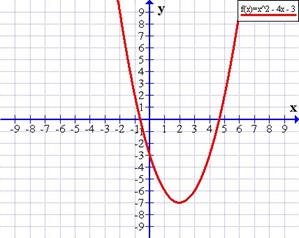
Dada la funcion cuadrática F(X)= x2-6x +8 determina:
A). Ha is donde de a abre la grafica
Se determina con el valor de a, si es positivo es hacia arriba y si es negativa es hacia abajo.
B). Si la ordenada del vértice es el mínimo o máximo valor.
Como es positiva es el mínimo, ya que a partir de ahí se va a abrir la parábola.
C). La intersección con el eje de Y.
Es igual a c, por lo que es 8.
D). Las intersecciones con X
Se sacan factorizando el trinomio, vamos a buscar 2 números que multiplicados de C y sumados B, al final les cambiamos el signo.
(X-2) (X-4); por lo que la intersección será X=2 y Y=4.
E). Las coordenadas del vértice.
Se saca con las fórmulas: H=-b/2a y R=F(h), las coordenadas serán (h,k). Por lo que:
h=-(-6)/2(1) =6/2 =3
Y K=32-6(3)+8
K=9-18+8
K=1
Por lo que el vértice es (3,-1)
F). Ecuación en la forma vértice.
Esta es y=a(X-b2) + K; de por lo que es y=1(X-3)2-1, que es igual a y=(X-3)2-1 ya que multiplicar por 1 no cambia el valor.
G). La ecuación del eje de simetría:
Es igual a H, por lo que es 3.
H). El valor mínimo de F(x)
Es igual a K, por lo que es -1.
I). El dominio.
Es el valor que puede tomar X, por lo que pueden ser todos los números reales. Dominio=R.
J). El rango de la función.
Es el valor que puede tomar Y, por lo que es igual a Y_> K, por lo que es Y_>–
1.
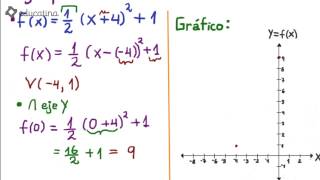
 Dom={R}.
Dom={R}.




